
Therefore, according to the table, if a company’s Z2 score is greater than 2.60, it’s currently safe from bankruptcy. The Z Score is for public manufacturing companies the Z1 Score is for private manufacturing companies, and the Z2 is for general use. To deal with these problems, Altman used his original data to calculate two modified versions of the Z Score, shown above. But since the Z Score expects a value that is common to manufacturing, it could be biased in such a way that a healthy jewelry store looks sick and a sickly grocery store looks healthy. Jewelry stores, for example, have a low asset turnover while grocery stores have a high turnover. This ratio varies significantly by industry.

The other problem is X5, Assets Turnover. Obviously, if a firm is not publicly traded, its equity has no market value. One of these ratios is X4, the Market Value of Equity divided by Total Liabilities. Two of the ratios shown in the figure have tended to limit the usefulness of the original Z Score measure. Summary - use in Six Sigma and Quality ControlĪ larger standard score indicates that the observation is more unlikely – and therefore indicates a problem.The table shows how these measures are used to calculate the three versions of the Z Score. So: the standard score supports comparing the significance of deviations observed in different populations. At worse than 1-in-5 odds of "just chance", you should check the drum manufacturing equipment for recent wear. If the standard score were 0.9, for example, then the probability that it is just a chance occurrence is 18%. Probably the z-score indicates that something has worsened recently. If the oil drum's standard score is higher than the measuring cup's, however, then the drum's equipment has the more serious problem – it is farther from average than the measuring cup's equipment. Now the measuring cup has the "larger" problem. What if the percentage error is smaller for the drum than the measuring cup? The 55-gallon drum (US gallons) holds 208.20 litres, so the percentage error is 0.019%. Clearly the drum is "more wrong", so the drum-making equipment is the higher priority. The measuring cup is off by 1 millilitre the drum by 40 millilitres. You need to decide where to deploy your scarce and valuable repair team. Each type of item should be its proper size. Let's say your company manufactures both measuring cups and oil drums. On the assumption that the population of data follows a normal "bell-shaped" curve, statisticians can show a relationship between the z-score and the Q probability. The ‘Q' probability expresses how likely an observation's value is to be a "random chance", rather than having a systemic cause.
The QA team may consider that there is no problem at this time. Therefore the probability, Q, that this standard score is due to chance is 42.3%. The QA team then reminds you that these measuring cups have a normal distribution. Your QA team assures you that the average of all the measuring cups is 1.00003 litres, and the standard deviation is 0.005. Is this a disaster? An anomaly? Acceptable? You check on one of these cups and find that it actually contains 1.001 litres.Ĭlearly, your measuring cup is wrong by 1 millilitre. Your quality assurance (QA) team tests each one and records what it really contains when filled to the "1 litre" mark. You and your customers expect them to be accurate. Let's say that your company manufactures measuring cups for household kitchens. What does the score mean for me? I mean, really? If you manufacture mirrors for Hubble-like telescopes, you would measure every one (several times). If you manufacture ball bearings, you probably don't measure each one. Statisticians like to point out that the "Student t-test" is more appropriate for incompletely-sampled populations.
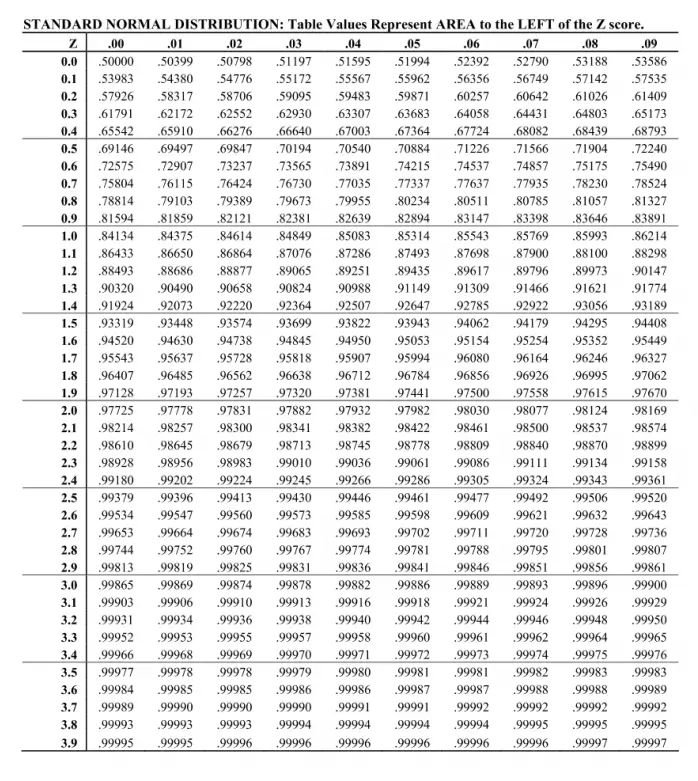
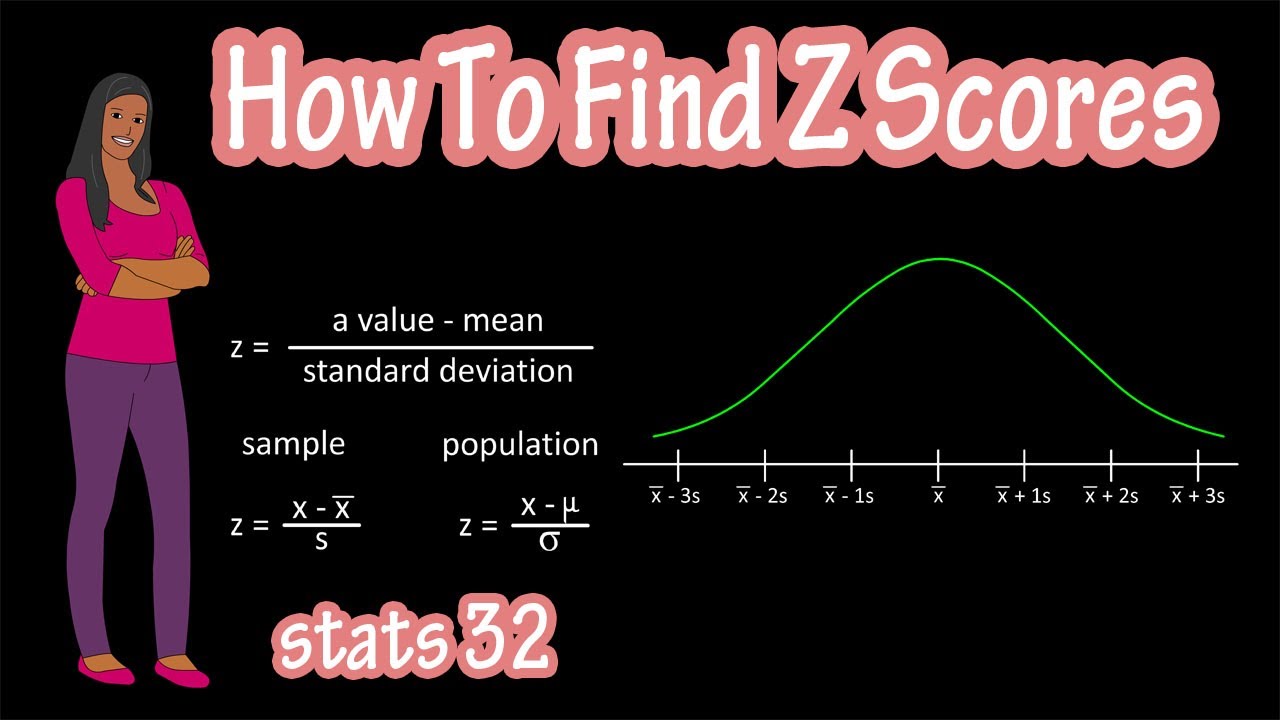
This is the sum of all observations, divided by the number of observations.m is the mean of the population: the average value.x is the "raw" score, to be standardized.The mathematical formula is: z = (x – m) / s, where: The "standard score", is the statistical measurement of "how far is one particular observation away from the standard deviation". Compute four different areas under the standard curve based on the z-value you enter.


 0 kommentar(er)
0 kommentar(er)
